Diagram 1
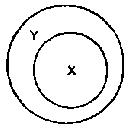 the larger circle representing Y and the smaller X
the larger circle representing Y and the smaller X
First let us examine some general statements and find out what their immediate implications are, i.e., find out to what other statements we are committed when we make them. We have learnt, shall we say, that a considerable knowledge of mathematics is a primary requisite for an actuary: then we may conclude, with some certainty, that:
This means that all those people classified as actuaries, i.e., all the members of the actuary class, are also members of the mathematician class, or, if you like, that the whole of the actuary class is included in the mathematician class. This is called a universal affirmative generalisation.
In order that we may apply the results of our investigations to classes of people or things other than actuaries and mathematicians, let us use symbols instead of names, and put this kind of generalisation or proposition, as the logicians call it, thus:
—it being understood that X stands for any class of persons or things that is wholly included in another class represented by Y. We shall also find it convenient to illustrate this proposition diagrammatically thus:
 the larger circle representing Y and the smaller X
the larger circle representing Y and the smaller X
Every generalisation, indeed every fact, can be expressed either in an affirmative or in a negative way. The form it takes will depend largely on the circumstances in which it is used, or the particular purpose it is intended to serve. Hence on one occasion we might say:
and on another:
but the meaning remains the same.
Hence when we assert that all actuaries are mathematicians, we are also committed to the assertion that:
or symbolically:
This form of the original proposition (1) is called the obverse, and the process of change is called obversion: in 2 we are, as it were, looking at 1 from a different point of view.
But in changing from the affirmative to the negative form of a proposition, or vice versa, it is very easy to fall into the error or fallacy known as illicit obversion and to draw unwarrantable conclusions. A careless and superficial thinker might easily be tempted to suppose that:
is equivalent to:
But careful reflection for a moment will show that no such inference is possible. A glance at diagram 1 will prove that it does not follow that people excluded from the X class are also necessarily excluded from the Y class. The negative equivalent of all citizens are qualified to vote is no citizen is disqualified to vote.
Now let us examine a universal negative generalisation like:
i.e., a statement that all members of the X class are wholly excluded from the Y class — diagrammatically
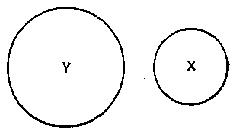
We can see first of all that the affirmative equivalent of this is:
but not
which would be a case of illicit obversion.
There is another process called conversion, by which the subject and the complement of certain propositions may be interchanged: e.g., it follows from 3 (look at diagram 2) that:
In other words total exclusion is a reversible relation — in excluding X from Y, we are also excluding Y from X.
But inclusion is not reversible: hence it follows that:
cannot be converted to:
If we did so we should fall into the error of illicit conversion. With diagram 1 in front of us, it is easy enough to see the fallacy; but illicit conversion is a commoner source of confusion than you would think. In the heat of debate it is easy enough to assume that a proposition which makes a universal statement about the subject also makes a universal statement about the complement, whereas, as diagram 1 should make clear, it is the word some which is understood before the complement. The proverb All that glitters is not gold is a warning against this fallacy: people fancy that because all gold glitters all that glitters is gold.
We have already had one example of this fallacy in Chapter Four, where a speaker is quoted as arguing that because all totalitarian states were planned states, advocacy of an extension of planning in this country was the equivalent to advocacy of totalitarianism. Let me give two other illustrations. The fact that the Nazis might have discovered that all the traitors they caught were Jews was no justification for concluding that all Jews were traitors—a conclusion they appeared to reach by some such reasoning process. Again, let us suppose that all the pacifists we have come across are also socialists, and that we have been rash enough to make the generalisation that all pacifists are socialists. It is not difficult to see that we may also be illogical enough to conclude from this that all socialists are pacifists.
On the other hand, proposition 1 is negatively convertible to:
i.e., if all actuaries are mathematicians, it follows that no one who is not a mathematician can be an actuary.
In the section on generalisation in Chapter Seven I have already urged the necessity of being chary of saying or implying all when we mean some, and of saying are when we mean may be or tend to be. Let us therefore examine the more cautious partial generalisations.
i.e., a statement that class X is partially included in class Y. Illustrated diagrammatically:
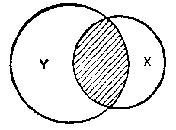
the larger circle representing Y and the smaller X.
Here the left-hand circle represents class Y, and the right-hand circle class X: the shaded portion representing the portion common to both.
It can be seen at once from this diagram that proposition 7 is simply convertible to:
But sometimes classes nearly coincide, and the portions of each outside the other are comparatively small, e.g.:
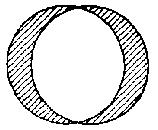
Let us suppose that in our experience the bulk of socialist opinion is also pacifist, and the bulk of pacifist opinion is also socialist. In the diagram above if the right-hand circle represents socialists and the left-hand pacifists, then the shaded portions represent (r) those socialists who are not pacifists, and (l) those pacifists who are not socialists. The diagram thus illustrates the propositions:
These are examples of partial negative generalisations.
It should be observed that although the same diagram may illustrate both, 10 is not equivalent to 9. 9 is consistent with, i.e., it does not exclude the possibility, that, some Y's are not X's; but it is also consistent with some Y's are X's. On the other hand 9 is negatively convertible to:
Let me make this clearer by another example. Starting from the proposition some teachers are not graduates, we can infer that some non-graduates are teachers. But we cannot infer therefrom that some graduates are not teachers or that some graduates are teachers, though we do not exclude the possibility of either.
All the propositions treated so far have been assertions referring directly to persons or things, their qualities and their relations, and representing our judgments about them. That is one aspect of thinking. But there is another aspect—already referred to in Chapter Seven, section 2—in which we pass from the noting of the qualities and characteristics of things to the discovery of connections between them—a step towards explaining things, towards the formulation of theories and laws. For example, in Chapter Four, we had occasion to note that people actuated by prejudices are liable to make logical errors. We then suspected that the presence of prejudice had some connection with the liability to make logical errors. In other words, we pass from the categorical assertion that (all) people actuated by prejudice are liable to make logical errors to:
And in doing so, we state that liability to make logical errors is a consequence of being actuated by prejudice, and that being actuated by prejudice is one antecedent condition of the liability to logical error. This is called a hypothetical proposition, and it has two parts: the if clause is known as the antecedent and the main clause as the consequent. Symbolically expressed, it will run:
Universal generalisations can usually be put in this way: e.g., (1) above would take the form:
It will be observed that this is not equivalent to saying:
Nor is it equivalent to saying:
If a person is not an actuary, he is not a mathematician or
If not X, then not Y : (the hypothetical form of illicit obversion).
All we can say is:
If a person is not a mathematician, he is not an actuary , or
If not Y, then not X .