So far we have been concerned with immediate inference only, and this is not strictly speaking deduction. Deduction involves applying the information contained in a proposition to a particular circumstance or set of circumstances, and drawing a conclusion different from the original proposition: that is, in the course of a deductive argument we move from one position to another in stages, and it is now our business to find out the forms these stages must take in order to make the conclusions arrived at valid, i.e., to make them reliable guides for action or further thought.
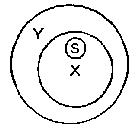
Let us therefore apply the statement (1) all actuaries are mathematicians to a particular person, Benjamin Smith. It tells you that if B.S. is on the actuarial staff of the Lifebuoy Assurance Co., you might safely infer that he would be able to help you to solve a mathematical problem. It also tells you that, if you know that if B.S. is not a mathematician, though he may be employed by the Lifebuoy Assurance Co., it will not be as an actuary. Let us represent Mr Smith by the symbol S: then symbolically these arguments run as follows:
(A)
1. All X's are Y's:
2. S is X:
3. therefore S is Y.

and
(B)
1. All X's are Y's:
2. S is not Y:
3. therefore S is not X.
Thus two items of information are put together—the first, the major premiss, in the form of a general statement, and the second, the minor premiss, in the form of a particular statement, and a third, called the conclusion, is deduced from them in the form of a particular statement. It will also be noticed that there are three terms (there cannot be more than three, see below), Y the major term, S the minor term, and X the middle term, and that the two premisses contain one common term (in the default of a common term no conclusion can be drawn).
It is also possible for both the major and the minor premisses to be general statements: in this case the conclusion will also be a general statement. Thus:
All non-utility garments are expensive:
all fur coats are non-utility garments:
Therefore all fur coats are expensive.
or
(C)
- All B are C:
- All A are B:
- therefore all A are C.
All these examples (A, B, and C) are valid deductive arguments in the form known as a syllogism. When I say that the reasoning is valid, I mean that the conclusion inevitably follows from the premisses, or, if you like, that the conclusion is entailed by the premisses. It does not necessarily follow that the conclusion is true: only when both premisses are true, is the conclusion also true. Whatever is entailed by true premisses is true — 'entailed' implying that the reasoning takes a valid form.
The form therefore of an argument or piece of reasoning is vitally important. But, you might say:
"Why all this fuss about forms? No one but a fool could fail to see that the reasoning in A, B, and C above is sound. It's as plain as a pikestaff."
Yes, perhaps too much fuss has been made in the past about the principles of deductive reasoning. The medieval school-men thought that deduction was the chief means of acquiring knowledge. We now realise that deduction can never teach us anything new: it can only tell us what is entailed by what we already know or assume.
But do not on that account underestimate the importance of form. When an argument is put in the form of a syllogism, or in another recognised structure, it is easy enough to tell whether it is sound or not. But unfortunately, we seldom put our arguments in a syllogistic form or in such a way that their essential structure is apparent. Very often, especially in a lengthy argument, we reason elliptically—hurrying on from one point to another, omitting a step here and there, and not stopping to make all the stages definite and explicit. We want to press on to our conclusion without wearying ourselves and making our hearers impatient by emphasising what we think ought to be obvious. In our hurry and impatience we thus tend to fall into confusion and error unwittingly; the sophist, on the other hand, deliberately glozes over or omits what is not obvious, and hopes to cover up his tracks by means of all the tricks of his trade.
"Sophistry," says Archbishop Whately, "like poison, is at once detected when presented to us in a concentrated form; but a fallacy which, when stated barely in a few sentences, would not deceive a child, may deceive half the world, if diluted in a quarto volume."
Even in a single piece of reasoning, we may omit a premiss (more often the major premiss), and sometimes the conclusion is left unstated and is left to the imagination. Again, before we get to the core of an argument, it is often necessary to strip it of irrelevancies, red-herrings, and rhetorical trimmings. In fact, it is pathetically easy to be misled unless we are able to distinguish and separate the form of an argument from its content. Hence we need to learn a little about practical logical technique to be able to reduce an argument to its essential structure and so find out whether it is valid or invalid. Having done this we can then turn to the content and consider whether the premisses and conclusion are true.
It cannot be sufficiently emphasised that not only may a perfectly logical argument be based on false premisses, but also true conclusions may be drawn as a result of unsound arguments. It is equally important that we should be able to detect both: the first, because otherwise we should be at the mercy of sophists or unscrupulous propagandists, who habitually argue logically from false premisses; and the second, because otherwise we might be tempted to condemn a conclusion as false on the ground that it was arrived at by bad logic.
Let us examine a few examples:
(a) All fungi are edible:
this is a fungus:
therefore this is edible.
Here the reasoning is sound. But the conclusion, if acted upon, might have serious consequences for you, for the major premiss is not true. But if the argument ran thus:
Some fungi are edible:
this is a fungus:
therefore this may be edible.
the reasoning is correct and the conclusion (for what it is worth) is true. It will at any rate induce caution, and perhaps lead to further investigation into the qualities of different kinds of fungi.
The major premiss in (a) is none other than a rash generalisation, arising from ignorance or limited experience. Enough has been said about this in Chapter Seven. All that I wish to emphasise here is that in putting forward arguments of this kind, we often omit the all in the major premiss, and yet proceed as if it were understood.
(b) All poisons are harmful:
alcohol is a poison:
therefore alcohol is harmful.
Again the reasoning is correct. But is the minor premiss true, stated thus in a categorical and wholesale manner? Does it not need modification in some such way as this? Alcohol, taken in immoderate quantities and in certain conditions, is a poison. The conclusion therefore, as it stands, is not in accordance with fact.
(c) Augustus was a Roman emperor:
Julius Caesar was a Roman general:
therefore Julius Caesar was the uncle of Augustus.
Here both premisses are true, and Julius Caesar was in fact the uncle of Augustus, but it does not follow from the premisses: see the conditions mentioned below (d).
(d) Loss of liberty makes men slaves:
I am denied the liberty of buying a glass of beer outside licensing hours:
therefore I am a slave.
Here the reasoning is invalid, because in a syllogism among the necessary conditions of validity are:
- that there should be no more than three terms,
- that there should be one term common to both premisses, and
- that the terms should not change their meaning or application during the course of the argument
—it is understood that the symbols used have the same referents throughout the argument. Now liberty in the major premiss means all liberty; but the liberty in the minor premiss refers to a single liberty: so there are in fact not three, but four terms, and there is no common term.
This is an example of the fallacy of equivocation — easy enough to detect when a simple instance like this is analysed and explained. But equivocal arguments are by no means uncommon: sometimes equivocation is committed involuntarily and may be due to haziness and to the neglect, through haste or impatience, of the precaution to define carefully the vital terms in an argument or discussion; but at other times it is committed deliberately with the intention to deceive, and is part of the stock-in-trade of the unscrupulous propagandist or the platform speaker or heckler who is more anxious to score a cheap debating point than to elucidate the truth. Sophistry of this kind often gains credence in readers or hearers who are blinded by prejudice or whose power of rational thought is neutralised by passion or strong feeling, or who are still superstitiously susceptible to the magic spell of words. But all these matters have been fully dealt with in Chapters Three and Four, and the reader is referred to these chapters again.
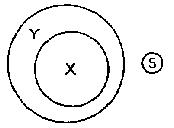
(e) All successful diplomats are noted for their tact:
Lord S. is noted for his tact:
therefore Lord S. is a successful diplomat.
i.e.
All X's are Y:
S is Y:
therefore S is X.
Here the conclusion may be true but it does not follow from the premisses — the reasoning is unsound. Reference to the diagram below will make this clear.
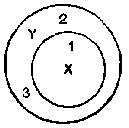
Thus S may be at any of the points numbered 1, 2, and 3 — not necessarily at 1, or at any other point within the circle X.
This type of fallacious argument may originate in a mistaken notion as to the immediate implications of the major premiss: the perpetrator of it may be first guilty of illicit conversion (q.v.), i.e., he may imagine that all X's are Y's is equivalent to all Y's are X's. Or it may originate in a confusion between all (and only) and all (but not only) . Or it may be due to his forgetting that Y's stand for some, not all, Y's.
But whatever the origin, it is a very common error. So also for similar reasons is the following:
(f) All Council houses are let at uneconomic rents:
These houses are not Council houses:
therefore these houses are not let at uneconomic rents.
or
All X's are Y's:
S's are not X's:
therefore S's are not Y's.
Again, reference to diagram 7 will make the error clear. By the minor premiss, S is excluded from circle X, but not necessarily also from circle Y. This error corresponds closely to illicit obversion (q.v.). Using the material of the example there quoted, the argument would run
All citizens are qualified to vote:
S is an alien (i.e., not a citizen):
therefore S is disqualified to vote.
Similar errors to (e) and (f) are possible in the hypothetical syllogistic forms. Before reading what follows, refer again to what has been said about hypothetical propositions. The hypothetical form of (A) is:
(D) If a person is an actuary, he is a mathematician:
S is an actuary: (i.e., the antecedent is affirmed)
therefore S is a mathematician.
or
If X, then Y:
S is X: (refer to diagram 5)
therefore S is Y.
and of (B):
(E) If a person is an actuary, he is a mathematician:
S is not a mathematician: (i.e., the consequent is denied)
therefore S is not an actuary.
or
If X, then Y:
S is not Y: (refer to diagram 6)
therefore S is not X.
Valid conclusions are arrived at in (D) and (E) when the antecedent is affirmed or when the consequent is denied, and these conclusions will be true only if the premisses are true.
Let us look at some further examples.
If a competitor cheats, he is disqualified:
the competitor S has cheated:
therefore he is disqualified.
Here the argument is sound — the antecedent is affirmed. But an incorrect and possibly untrue deduction would be made if, instead of affirming the antecedent, you affirmed the consequent, and argued:
If a competitor cheats, he is disqualified:
the competitor S is disqualified:
therefore the competitor S has cheated
because cheating, the condition here mentioned for disqualification, is not necessarily the sole condition: the competitor may have broken some other rule.
Affirming the consequent is a very common source of fallacious reasoning and underlies the post hoc ergo propter hoc fallacy: it assumes that a consequence has only one condition or cause to account for it.
Nevertheless, the cumulative use of such reasoning is often the only resource in solving a mystery when direct evidence — testimonial evidence — is lacking, and in testing a hypothesis to find out whether it accounts for all the relevant data. Hence it is extensively used in detection and in building up what is called circumstantial evidence. Look back to Chapter Two where stage 4 of the thinking process is elaborated. The detective there is confronted with a number of data — all suspected effects or consequences of some cause or condition he is trying to discover. A cause or condition to account for them is suggested to him. He then argues after this fashion:
If X, then Y1, Y2, Y3. Y4, . . . and so on
But Y1, Y2, Y3, etc. (i.e., affirming the consequent)
therefore X:
X being the suggested cause or condition and Y1....etc., being the probable results of X. If all these results are confirmed by observation, and if there are no other relevant data discoverable that point to a different cause, then X is probably true.
But X will remain at best probable in default of actual proof by way of experiment. For example, the Medical Officer mentioned in Chapter Two argued thus:
If the epidemic was caused by contamination of milk, then the incidence of the epidemic will correspond to the usual round of some milk retailer: the houses affected are all served by the same milk retailer: (i.e., affirming the consequent.) therefore the epidemic was probably caused by milk contamination.
But he could not be sure until he had subsequently taken steps to stop the supply of milk from that source and had found that the removal of the suspected cause was followed by the discontinuance of the effect.
As you no doubt have already gathered, if my explanation has been sufficiently clear, this process of reasoning is not deductive, but inductive. The principles of valid deduction tell us that what is entailed by true premisses must be true. But Y1, Y2, Y3, are not entailed by X, in the sense in which this word has been used, i.e., they are not solely and inevitably caused by X: they only indicate or point to X. Circumstantial evidence, as you know, may be delusive: subsequent investigation and discovery may result in unearthing a fact that entirely upsets a theory, however elaborately built up in its absence. That classic of detective fiction, Mr E. C. Bentley's Trent's Last Case, provides a very good example.
After this digression, let us turn to the second hypothetical syllogism (E). A correct conclusion is arrived at if the consequent is denied. This form of argument is also very commonly used in scientific investigation into causes: if the expected effect does not occur, then the suggested cause can be ruled out. This is how the Medical Officer tested and rejected his first hypothesis he argued thus:
If the epidemic was caused by simple infection from patient to patient, then the outbreak would be gradual and spread from family to family: (If X, then Y.)
but the outbreak was sudden and whole families were affected simultaneously : (Not Y.)
therefore the epidemic was not caused by simple infection from patient to patient. (therefore not X.)
But if the antecedent is denied, nothing conclusive follows: the effect is similar to that in (f) and in illicit obversion: e.g.
If a person is actuated by prejudice, he is liable to make logical errors
But S is not actuated by prejudice:
therefore S is not liable to make logical errors.
As you can see, liability to make logical errors may be due to sources other than prejudice: it may be due to ignorance, or excessive zeal, or carelessness. Reference to diagram 7 will prove that exclusion from the X circle does not necessarily involve exclusion from the Y circle.